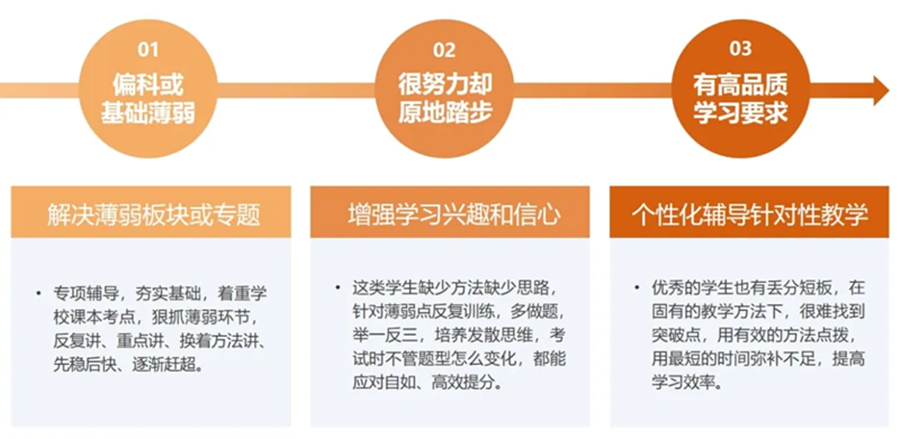
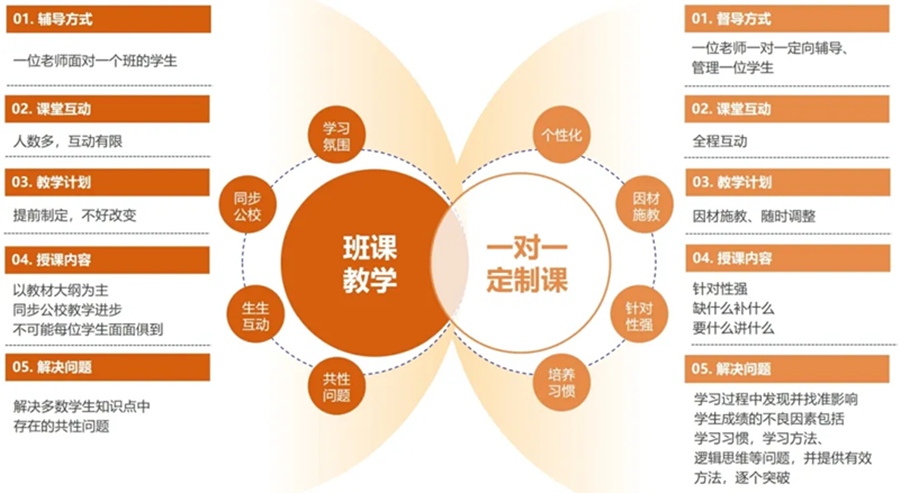
高中阶段的数学学习,既是逻辑思维的进阶修炼,也是升学路上的关键战场。函数的抽象、几何的严谨、概率的精妙,每一个模块都考验着学子的理解力与应用力;而高考的压力、知识的深度、题型的多变,更让不少同学在数学学习中陷入困惑 —— 明明课堂听懂了,解题却无从下手;明明刷题无数,分数却难以突破瓶颈。
1、太原新东方教育 2、太原辰星教育 3、太原学大教育 4、太原宏楼教育 5、太原锐思教育 6、太原华英教育 7、太原高途教育 8、太原龙文教育 9、太原精锐教育 10、太原美博教育 以上机构排名来源网络非官方顺序,不分先后,仅供参考! 新东方中小学一对一学习中心,依托新东方强大的品牌资源和教学优势,整合丰富的一对一辅导经验、深受学员及家长信赖的优秀教师团队,为您护航高考,决胜高考之巅。 高中数学的所有难题,本质都是基础知识点的综合与变形。基础不牢,后续学习只会越学越吃力。 精读教材,吃透定义与定理 不要跳过教材直接刷题!数学教材的定义、定理、公式是核心,不仅要记住,更要弄懂 “为什么”:比如推导等差数列通项公式的 “累加法” 逻辑,理解函数单调性定义中 “任意 x₁<x₂” 的严谨性。 动手推导公式:比如三角函数的诱导公式、立体几何的体积公式,自己推导一遍,比单纯背诵记得更牢,还能掌握推导过程中的思维方法(如数形结合、转化与化归)。 建立 “知识树”,串联模块关联 高中数学核心模块(函数、几何、概率、数列、导数、解析几何等)不是孤立的,要主动梳理关联:比如 “函数单调性” 可用于解决数列的增减性、导数的极值问题;“向量” 既能连接平面几何,也能辅助解析几何运算。 用思维导图工具(如 XMind、手写笔记)整理模块框架:比如 “函数” 模块下,分定义域、值域、单调性、奇偶性、周期性、图像变换、常见题型(分段函数、复合函数)等分支,每个分支标注关键知识点和易错点。 基础题型 “零失误”,拒绝 “眼会手不会” 教材课后习题、基础练习题是检验基础的最佳载体,务必独立完成,确保简单题(选择前 6 题、填空前 3 题、解答前 2 题)不丢分。 遇到基础错题,标注 “知识点漏洞”(如 “对数定义域忘记大于 0”“等差数列首项判断错误”),针对性补教材例题,直到同类题能快速做对。 二、解题提升:从 “会做一道题” 到 “会解一类题” 高中数学题型有限,盲目刷题不如精准归类,掌握 “解题模型” 和 “思维方法”。 分类刷题,总结 “题型模板” 例:导数 “恒成立问题”→ 常见模板:分离参数法、构造函数求最值、分类讨论单调性; 例:解析几何 “弦长问题”→ 模板:联立方程→判别式判断→韦达定理→弦长公式(√(1+k²)|x₁-x₂|)。 按模块分类刷题(如 “函数单调性题型”“立体几何证明题型”“导数恒成立问题”),每类题集中做 10-20 道,总结共性解法: 建立 “题型笔记本”,记录每类题的 “解题步骤 + 关键思路 + 易错点”,比如 “立体几何求角”,区分 “异面直线夹角”“线面角”“二面角” 的不同解法(平移法、投影法、空间向量法)。 掌握 “核心思维方法”,突破难题瓶颈 高中数学 80% 的难题,都离不开以下 5 种思维方法,要主动在解题中运用: 数形结合:函数问题画图像、几何问题建坐标系、不等式问题用数轴,把抽象问题直观化(比如用函数图像判断方程根的个数); 转化与化归:把复杂问题变简单(如把 “不等式恒成立” 转化为 “函数最值问题”,把 “立体几何证明” 转化为 “平面几何问题”); 分类讨论:遇到含参数、图形不确定的题(如二次函数对称轴位置、直线斜率存在与否),按标准分类,避免漏解; 建模思想:概率统计、实际应用问题,先提炼数学模型(如古典概型、线性规划),再代入求解; 逆向思维:正面解题困难时,从结论倒推(如证明题用反证法,排列组合题用 “总情况 - 不符合情况”)。 限时训练,提升 “解题速度” 高中数学考试时间紧(120 分钟做 150 分题目),平时练习要限时:选择填空控制在 40 分钟内,解答题每道题不超过 10 分钟,避免 “平时做得出,考场做不完”。 优先练 “解题技巧”:比如选择填空用特殊值法、排除法、估算法快速得出答案(如判断函数奇偶性,代入 x=1 和 x=-1 验证),节省时间给难题。 三、错题复盘:让 “错误” 成为提分关键 错题是最宝贵的 “提分资源”,比盲目刷 10 道新题更有效。核心是 “揪出根源,避免重复犯错”。 建立 “错题本”,按 “错误类型” 分类 知识漏洞:没掌握某个知识点(如 “不清楚双曲线的渐近线公式”); 方法不当:思路错了(如 “立体几何没想到用空间向量”); 计算失误:粗心、步骤遗漏(如 “导数求导漏项”“解方程移项变号错误”); 审题错误:没看清条件(如 “题目说‘单调递增’,看成‘单调区间’”); 错题本不是抄题本,要记录 3 个核心信息: 原题(或关键条件)+ 错误答案; 错误原因(分 4 类标注): 正确解法 + 优化思路(如 “这道题用分离参数法比分类讨论更简单”)。 定期复盘,实现 “错题清零” 第一遍:重做所有错题,若能快速做对,标记 “已掌握”; 第二遍:只做 “未掌握” 的错题,直到同类题不再出错; 考前 1 周:重点看 “计算失误” 和 “审题错误” 类错题,提醒自己考场避坑。 每周花 1-2 小时复盘错题本: 同类题 “二次练习”,强化记忆 遇到错题后,找 2-3 道同类题针对性练习(比如错题是 “导数极值点偏移问题”,就集中练这类题),确保掌握解题逻辑,而不是记住答案。